1. 傅里叶变换
傅里叶变换是将时域信号变换到频域,以方便进一步的分析和处理。傅里叶逆变换是将信号从频域变换到时域。
傅里叶变换后,频域的基本单元为正弦波信号,傅里叶变换的就是原始信号变换成许多不同频率,不同幅值的正弦波组合。
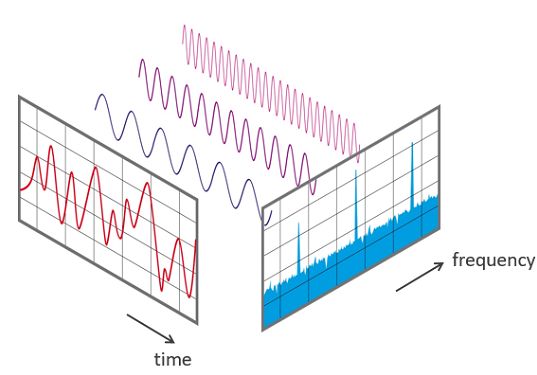
信号分解:
$$f(t)=\sum_{n=1}^{\infty}A_n\cos{n\omega_0+\phi_n}+B$$
傅里叶变换:
$$F(w)=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt$$
信号组合:
$$f(t)=\sum_{-\infty}^{+\infty}F(n\omega_0)e^{j\omega_0 t}$$
傅里叶逆变换:
$$f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(\omega)e^{j\omega t}d\omega$$
2. 拉普拉斯变换
傅里叶分解后,使用的正弦信号为等幅信号,也就是任意频率分量的幅值始终不变。如果原始信号在无穷远处的幅值无限增加,那么该信号显然无法用等幅的正弦信号组合而成,此时需要使用拉普拉斯变换。拉普拉斯变换是在原先傅里叶变换的基础上乘了一个因子而改善得到的,拉普拉斯变换的适用范围更广,可以将傅里叶变换视为拉普拉斯变换的一种特殊形式。
拉普拉斯变换公式如下:
$$F(s)=\int_{-\infty}^{+\infty}f(t)e^{-st}dt$$
其中 $s=\sigma+j\omega$ 展开得展开式:
$$F(w)=\int_{-\infty}^{+\infty}f(t)e^{-\sigma t}e^{-j\omega t}dt$$
如何将 $f(t)$ 与 $e^{-\sigma t}$ 组合,则为将原始信号进行衰减。由于 $e^{-\sigma t}$ 的衰减能力足够强,能够将更多类型的信号掰弯,因此拉普拉斯变换的适用范围比傅里叶变换广。
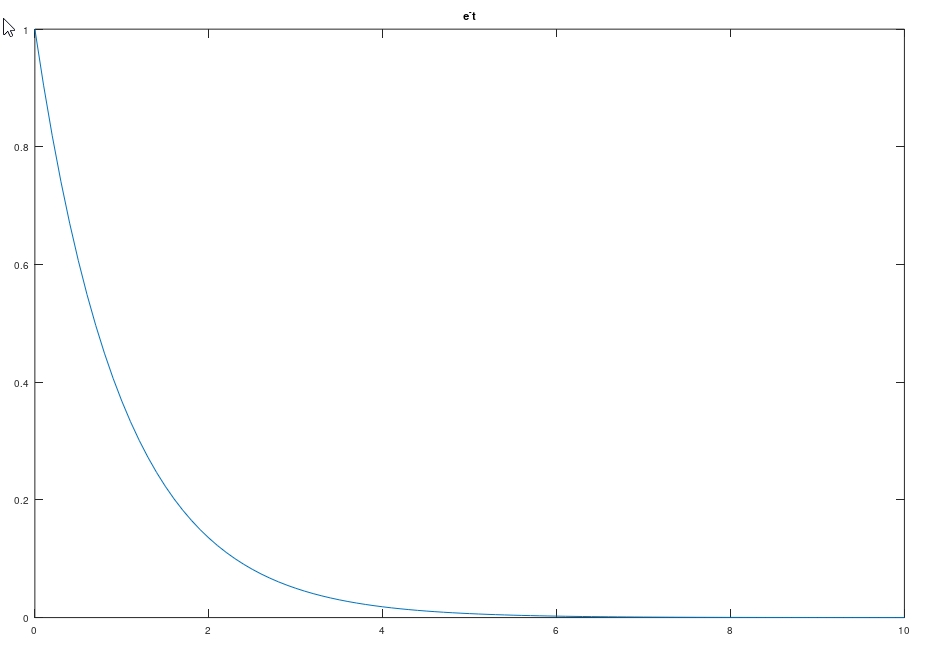
如果将 $e^{-j\omega t}$ 与 $e^{-\sigma t}$ 组合,则随时间变化改变了正弦信号的幅值,因此能组合出更多类型的原始信号。
3. Z 变换
Z 变换的实质是将离散的采样信号用多组不同频率和幅值离散的正弦点去表达,也就是拉普拉斯变换的离散表达:
$$\begin{split} F_s(s)=\int_{0}^{\infty}[\sum_{n=0}^{\infty}f(nT)\delta(t-nT)]e^{-st}dt \ =\sum_{n=0}^{\infty}f(nT)e^{-snT} \ \end{split}$$
令 $Z=e^st$,则
$$=\sum_{n=0}^{\infty}f(nT)Z^{-n}$$
以上公式的自变量 s 为拉普拉斯变换的 s,下角标 s 代表离散采样。$e^{-snT}=Z^{-n}$ 即为所述的离散正弦信号点。
「真诚赞赏,手留余香」
真诚赞赏,手留余香
使用微信扫描二维码完成支付
